INSIDE
RACING
T E C H N O L O G Y
IRT Home
IRT Home
News Page
Contents Page
Newsletter &
Books
email Paul
Aerodynamic Drag
You Don’t Get Something for Nothing
Mount a wing upside down on your racecar and, when the car moves through the air, the wing will press the car to the track surface, giving more grip. But it’s not free. Just as airplane engines are needed to overcome the drag of the plane, a racecar engine has to overcome the drag of the car, including the wings.
There is a basic equation for the force it takes to push something through air:
In this equation, D is the density of the air, A is the frontal area of the moving shape, and V is its velocity relative to the air.
For real body shapes, air at standard conditions, A in square ft., V in mph, and drag in pounds of force, this equation becomes:
This equation shows that to calculate drag you need to know three things: Cd, the drag coefficient; A, the frontal area of whatever you’re driving through the air; and the speed of air past it. This equation shows an important point—aerodynamic forces are proportional to the square of the speed. That means you quadruple the drag or lift when you double the speed.
The drag coefficient, Cd, is important because, in concert with frontal area, it determines the power cost of pushing a shape through air at a certain speed. A small, low-Cd road car will have a higher top speed than a larger, boxier car with the same engine power.
Here are measured drag coefficients for some basic shapes. These numbers come from tests of shapes with known cross sectional areas. You blow air over them and measure the force on the shape. That’s what wind tunnels do. The arrow in front of the shape gives the direction of the air blowing over the shape. The cone shape, for example, would have a lower Cd if it were rotated so the air saw the flat end first.
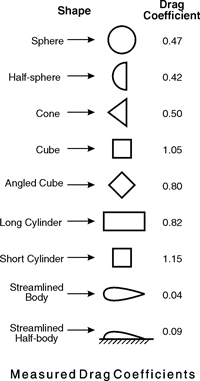
Notice the difference in the Cd of a long and short cylinder. You probably know that a slippery road car has a Cd of about 0.32. A chunky one is 0.38.